Benchmarks
Test computer-
- Apple MacBook Pro
- 2.4 Ghz
- Intel core i5
- OSX 10.7.2
Speed test. Generate 2^32 random numbers with Discordia.
Keyed with "hi there<cr><^d>" Time measured with the UNIX
time command is 34 minutes or 2.1 million random bytes generated a second.
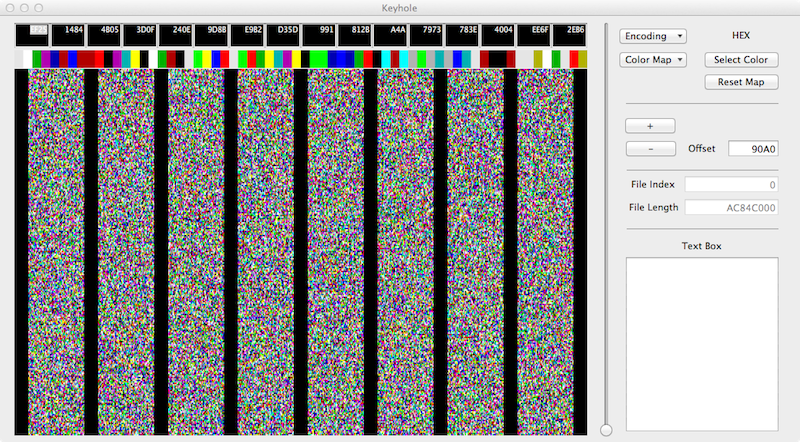
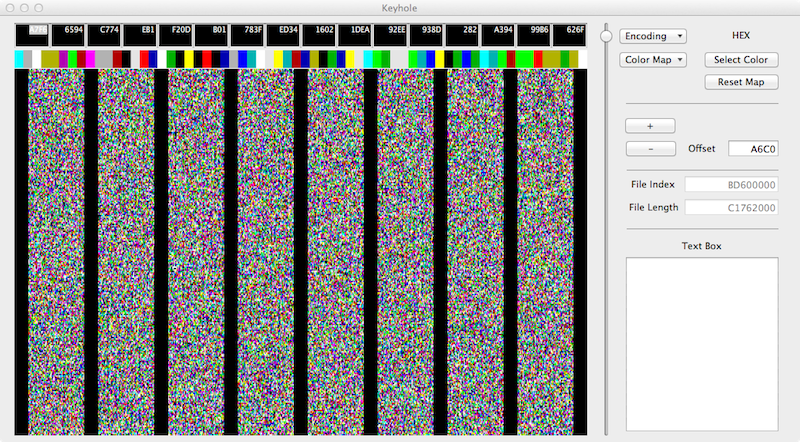
Visual inspection of random numbers generated with my Keyhole program.
Numbers at the beginning of a 2^32 generation run-
Numbers at about the 3 Gig mark-
Discordia 1.1 having problems-

The algorithm for Keyhole is simple-
- Read a byte from a file
- Break the byte into 2 four bit nibbles.
- Assign one of 16 standard colors to each nibble.
- Plot the colors on the screen
- In the above examples the screen resolution is 64K bytes.
- Each collum represents 0x2000 bytes.
During development of the Chaotic Random Core, the Ent program was used
extensively in order to get a sense of direction. Dieharder was
then used.
Ent and Dieharder were benchmarked with 20K bytes of "noise" from
random.org. The gpg implementation of AES (with compression) was
also used as a bench mark.
The Chaotic Random Core output compares favorabely with the benchmarks generated with data from random.org.
AES tended to do better on Dieharder with the least number of "weak"
results. However on long generation runs the chi square
distribution of AES falls flat as far as randomly exceeding the
calculated value as reported by Ent. With the Chaotic Random
Core, if the chi square distribution hangs around 255 and randomly
exceeds it 50% of the time, the rest of the numbers reported by ent
also tend to look good.
Return to main page.




